首发于 微信公众号 Mumu的小宇宙 2025.08.14
目录
- 背景信息说明
- 任务1解释
- 任务2解释
- 从报告看到什么
背景
昨天发表了文章《投资多久必赚钱?(基于李笑来Github仓库)》,里面的代码涉及到两个任务,今天用一片文章来解析一下两个任务到底是什么意思以及报告的内容。
我们以S&P500为例:
基准年份 1926
- 使用数据范围: 1926–2024
- 选择列: Return (%)
任务1 (无损失期限): 最小L = 15年; 最差窗口 1929–1943; 累计收益率 = 10.10%; 测试窗口数 = 1380
任务2 (τ = 0.5%): 最小L = 97年; 最小 1926–2022 (年化收益率 10.12%); 最大 1927–2023 (年化收益率 10.26%); 差值 0.14%; 测试窗口数 = 4947
任务2 (τ = 1.0%): 最小L = 94年; 最小 1929–2022 (年化收益率 9.54%); 最大 1931–2024 (年化收益率 10.51%); 差值 0.97%; 测试窗口数 = 4935
任务2 (τ = 1.5%): 最小L = 71年; 最小 1930–2000 (年化收益率 10.61%); 最大 1933–2003 (年化收益率 11.88%); 差值 1.28%; 测试窗口数 = 4544
基准年份 1957
- 使用数据范围: 1957–2024
- 选择列: Return (%)
任务1 (无损失期限): 最小L = 11年; 最差窗口 2000–2010; 累计收益率 = 4.57%; 测试窗口数 = 693
任务2 (τ = 0.5%): 最小L = 65年; 最小 1959–2023 (年化收益率 10.27%); 最大 1957–2021 (年化收益率 10.63%); 差值 0.36%; 测试窗口数 = 2340
任务2 (τ = 1.0%): 最小L = 56年; 最小 1957–2012 (年化收益率 9.70%); 最大 1969–2024 (年化收益率 10.57%); 差值 0.87%; 测试窗口数 = 2268
任务2 (τ = 1.5%): 最小L = 55年; 最小 1957–2011 (年化收益率 9.59%); 最大 1970–2024 (年化收益率 10.95%); 差值 1.36%; 测试窗口数 = 2255
基准年份 1972
- 使用数据范围: 1972–2024
- 选择列: Return (%)
任务1 (无损失期限): 最小L = 11年; 最差窗口 2000–2010; 累计收益率 = 4.57%; 测试窗口数 = 528
任务2 (τ = 0.5%): 最小L = 52年; 最小 1972–2023 (年化收益率 10.77%); 最大 1973–2024 (年化收益率 10.87%); 差值 0.11%; 测试窗口数 = 1430
任务2 (τ = 1.0%): 最小L = 51年; 最小 1972–2022 (年化收益率 10.48%); 最大 1974–2024 (年化收益率 11.44%); 差值 0.96%; 测试窗口数 = 1428
任务2 (τ = 1.5%): 最小L = 48年; 最小 1973–2020 (年化收益率 10.65%); 最大 1975–2022 (年化收益率 11.85%); 差值 1.20%; 测试窗口数 = 1416
基准年份 1984
- 使用数据范围: 1984–2024
- 选择列: Return (%)
任务1 (无损失期限): 最小L = 11年; 最差窗口 2000–2010; 累计收益率 = 4.57%; 测试窗口数 = 396
任务2 (τ = 0.5%): 最小L = 39年; 最小 1984–2022 (年化收益率 10.97%); 最大 1985–2023 (年化收益率 11.46%); 差值 0.49%; 测试窗口数 = 858
任务2 (τ = 1.0%): 最小L = 35年; 最小 1988–2022 (年化收益率 10.52%); 最大 1985–2019 (年化收益率 11.39%); 差值 0.88%; 测试窗口数 = 840
任务2 (τ = 1.5%): 最小L = 28年; 最小 1996–2023 (年化收益率 9.60%); 最大 1994–2021 (年化收益率 10.78%); 差值 1.17%; 测试窗口数 = 770
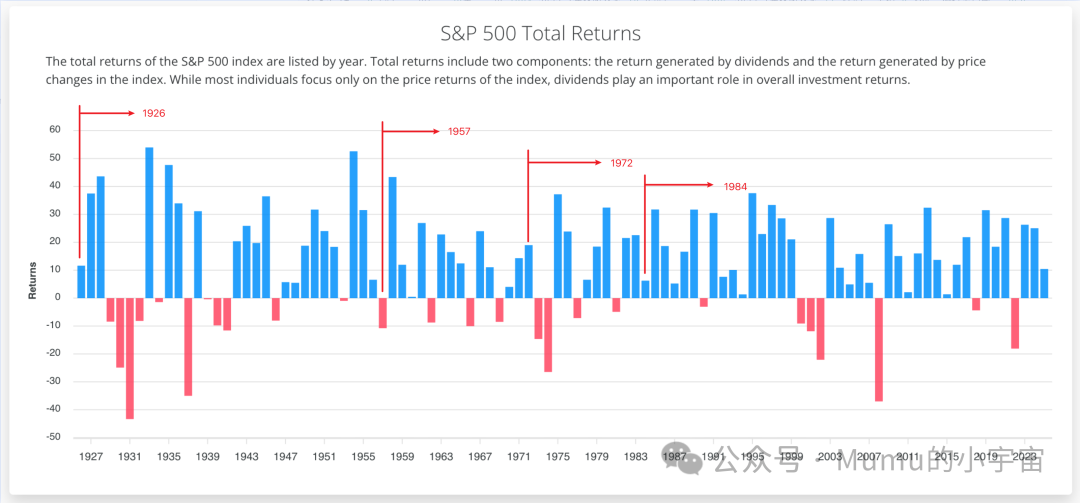
原始数据是1926年-2024年的年化收益率,然后代码设定了4个基准年份,分别是:1926年、1957年、1972年、1984年,也就是对应着下图的几个时间窗口的年化收益率:
任务1:无损失期限
我们聚焦到其中一个时间窗口来看具体的任务,比如1926-2024:
基准年份 1926
- 使用数据范围: 1926–2024
- 选择列: Return (%)
任务1 (无损失期限): 最小L = 15年; 最差窗口 1929–1943; 累计收益率 = 10.10%; 测试窗口数 = 1380
任务2 (τ = 0.5%): 最小L = 97年; 最小 1926–2022 (年化收益率 10.12%); 最大 1927–2023 (年化收益率 10.26%); 差值 0.14%; 测试窗口数 = 4947
任务2 (τ = 1.0%): 最小L = 94年; 最小 1929–2022 (年化收益率 9.54%); 最大 1931–2024 (年化收益率 10.51%); 差值 0.97%; 测试窗口数 = 4935
任务2 (τ = 1.5%): 最小L = 71年; 最小 1930–2000 (年化收益率 10.61%); 最大 1933–2003 (年化收益率 11.88%); 差值 1.28%; 测试窗口数 = 4544
在1926年-2024年这段时间里,如果我们用每1年来看,有的年份是蓝色的柱子盈利,有的年份是红色的柱子亏损,也就是说,持有1年来看,不能保证必定盈利;
如果选择两年,比如1926-1927,我们可以看到是两个蓝色的柱子,也就都是盈利的,但是如果1929年买入,持有1929-1930年,这两年就都是红色的柱子,也就都是亏损的;
以此类推,会有一个年数,当我持有这些年时,从任意一年买入,都会是盈利的,比如从上图看上去,1929年开始连续4年是红柱子,然后没过几年又有几根红柱子,也就是从1929年开始,我持有15年,也会是正收益,而且是10.10%,也就是下面这一条的内容:
任务1 (无损失期限): 最小L = 15年; 最差窗口 1929–1943; 累计收益率 = 10.10%; 测试窗口数 = 1380
所以,任务1告诉我们的是,无损失,需要多少年。
我们也来核算一下结果:
原始数据:
年份,收益率
1944,19.75
1943,25.90
1942,20.34
1941,-11.59
1940,-9.78
1939,-0.41
1938,31.12
1937,-35.03
1936,33.92
1935,47.67
1934,-1.44
1933,53.99
1932,-8.19
1931,-43.34
1930,-24.90
1929,-8.42
我们用笨办法计算一下:
第1年:100*(1-8.42%)=91.58
第2年:91.58*(1-24.9%)=68.777
第3年:68.777*(1-43.34%)=38.969
第4年:38.969*(1-8.19%)=35.777
第5年:35.777*(1+53.99%)=55.093
第6年:55.093*(1-1.44%)=54.3
第7年:54.3*(1+47.67%)=80.185
第8年:80.185*(1+33.92%)=107.384
第9年:107.384*(1-35.03%)=69.767
第10年:69.767*(1+31.12%)=91.478
第11年:91.478*(1-0.41%)=91.103
第12年:91.103*(1-9.78%)=82.193
第13年:82.193*(1-11.59%)=72.667
第14年:72.667*(1+20.34%)=87.447
第15年:87.447*(1+25.9%)=110.0958
第16年:110.0958*(1+19.75%)=131.84
可以看到,在第8年时,短暂回本,之后又进入到了副收益,直到第15年、16年,持续正收益,所以从第15年看,收益是10.0958,注意,这是累积收益率,不是年化收益率。
如果计算年化收益率应该是:(110.0958/100)^(1/15)-1=0.643%
任务2
任务2: “稳定收益”的投资期限
我们还是聚焦到其中一个时间窗口来看具体的任务,比如1926-2024:
基准年份 1926
- 使用数据范围: 1926–2024
- 选择列: Return (%)
任务1 (无损失期限): 最小L = 15年; 最差窗口 1929–1943; 累计收益率 = 10.10%; 测试窗口数 = 1380
任务2 (τ = 0.5%): 最小L = 97年; 最小 1926–2022 (年化收益率 10.12%); 最大 1927–2023 (年化收益率 10.26%); 差值 0.14%; 测试窗口数 = 4947
任务2 (τ = 1.0%): 最小L = 94年; 最小 1929–2022 (年化收益率 9.54%); 最大 1931–2024 (年化收益率 10.51%); 差值 0.97%; 测试窗口数 = 4935
任务2 (τ = 1.5%): 最小L = 71年; 最小 1930–2000 (年化收益率 10.61%); 最大 1933–2003 (年化收益率 11.88%); 差值 1.28%; 测试窗口数 = 4544
任意设定一个投资期限,我们会获得这个投资期限的年化收益率,比如还是用上面的1929-1944年的数据:
年份,收益率
1944,19.75
1943,25.90
1942,20.34
1941,-11.59
1940,-9.78
1939,-0.41
1938,31.12
1937,-35.03
1936,33.92
1935,47.67
1934,-1.44
1933,53.99
1932,-8.19
1931,-43.34
1930,-24.90
1929,-8.42
为了说明任务2做的事,我们取3年作为投资期限计算一下,比如:1929-1931,1930-1932,1931-1933
1929-1931:(38.969/100)^(1/3)-1=-0.27
- 1929: 100*(1-8.42%)=91.58
- 1930: 91.58*(1-24.9%)=68.777
- 1931: 68.777*(1-43.34%)=38.969
1930-1932:(39.067/100)^(1/3)-1=-0.269
- 1930: 100*(1-24.9%)=75.1
- 1931: 75.1*(1-43.34%)=42.552
- 1932: 42.552*(1-8.19%)=39.067
1931-1933:(80.105/100)^(1/3)-1=-0.0713
- 1931: 100*(1-43.34%)=56.66
- 1932: 56.66*(1-8.19%)=52.0195
- 1933: 52.0195*(1+53.99%)=80.105
从上面的数据,我们可以看到,1929-1931 vs 1930-1932,相差0.001,但是1930-1932 vs 1931-1933,相差19.77,收益是十分不稳定,波动剧烈的。
这是用3年的投资期限,如果我们拉长这个投资期限,去“抹平”那些收益率剧烈波动的年份,就会得到一个相差较小的收益率。
任务2 (τ = 0.5%): 最小L = 97年; 最小 1926–2022 (年化收益率 10.12%); 最大 1927–2023 (年化收益率 10.26%); 差值 0.14%; 测试窗口数 = 4947
任务2 (τ = 1.0%): 最小L = 94年; 最小 1929–2022 (年化收益率 9.54%); 最大 1931–2024 (年化收益率 10.51%); 差值 0.97%; 测试窗口数 = 4935
任务2 (τ = 1.5%): 最小L = 71年; 最小 1930–2000 (年化收益率 10.61%); 最大 1933–2003 (年化收益率 11.88%); 差值 1.28%; 测试窗口数 = 4544
如果我们设定波动率为0.5%,97年可以让收益变得稳定;
如果我们设定波动率为1.0%,94年可以让收益变得稳定;
如果我们设定波动率为1.5%,71年可以让收益变得稳定。
如果我们选取1984-2024:
基准年份 1984
- 使用数据范围: 1984–2024
- 选择列: Return (%)
任务1 (无损失期限): 最小L = 11年; 最差窗口 2000–2010; 累计收益率 = 4.57%; 测试窗口数 = 396
任务2 (τ = 0.5%): 最小L = 39年; 最小 1984–2022 (年化收益率 10.97%); 最大 1985–2023 (年化收益率 11.46%); 差值 0.49%; 测试窗口数 = 858
任务2 (τ = 1.0%): 最小L = 35年; 最小 1988–2022 (年化收益率 10.52%); 最大 1985–2019 (年化收益率 11.39%); 差值 0.88%; 测试窗口数 = 840
任务2 (τ = 1.5%): 最小L = 28年; 最小 1996–2023 (年化收益率 9.60%); 最大 1994–2021 (年化收益率 10.78%); 差值 1.17%; 测试窗口数 = 770
同样设定波动率为1.5%,28年就可以让收益变得稳定。
从报告看到什么
这时,我们再来整体看看报告:
横向来看,无损失期限变短了,仅仅11年就变得无亏损了,而且后几个基准年份都出现在互联网泡沫阶段2000-2010年,收益变稳定的速度呈现了越来越快的趋势,即便把波动率放宽到1.5%,以1984年作为基准,最小的年化收益率也有9.6%。
随着科技的发展,信息同步越来越高效,资金流动、调控越来越高效,资金的步调协调周期越来越短。
如果我们再看看科技股为主的纳斯达克100,我们设定了不同的时间基准:
1986:接近指数创立时间(1985年创立)1995:互联网时代和科技革命前夕2000:科技泡沫顶峰,最坏情况测试2010:金融危机后复苏起点
我们可以看到,资金协调的时间也在变得越来越短,我们用纳斯达克100,2010年后的数据进行一个乐观又不失理性的估计,持有15年可获得稳定的17%+的年化收益率。
这就给了我们一个具有实践意义的参考值。
在《您到底需要多少钱?》一篇文章中我们提到,不防先以216万作为目标,如果我们结合15年,年化17%的结果,我们可以过什么日子?
从216万中拿出195万,这195万可以每年花13万,花15年;
剩余的21万,买入纳斯达克100,年化17%,持有15年,21万变成了221万;
从221万中再拿出195万;
剩余的26万,再买入纳斯达克100,持有15年;
再拿出195万;
再持有15年;
再拿出…;
再持有…;
再…;
…
恭喜你,如果觉得不够,就持有再长点,放的再多点。
扫码加入Mumu的小宇宙

 投资多久必赚钱?(基于李笑来Github仓库)
投资多久必赚钱?(基于李笑来Github仓库)
 您到底需要多少钱?
您到底需要多少钱?
 如何提前检验最低财富自由的生活?
如何提前检验最低财富自由的生活?
 冯晓东——Mixin Network 被黑及开发情况说明(文字版)
冯晓东——Mixin Network 被黑及开发情况说明(文字版)
 将Mixin交易记录保存到本地
将Mixin交易记录保存到本地